Questions
FAQ's about Power Function and Critical-Error Graphs
Frequently-Asked-Questions about Power Function Graphs and Critical-Error Graphs
Frequently Asked Questions about Power Function Graphs and Critical-Error Graphs
- Why aren't actual concentration units used on the x-axis?
- Why is the y-axis given as probability instead of average run length (ARL)?
- Why aren't the power curves smooth?
- How good are the probabilities estimated by computer simulations?
 Why aren't actual concentration units used on the x-axis?
Why aren't actual concentration units used on the x-axis?
The x-axis is presented in units that are multiples of the standard deviation of the method in order to normalize the graphs and make them applicable to any test in any laboratory. If actual concentration units were used, it would be necessary to generate specific graphs for each test in each laboratory. This would mean each laboratory would need the capability of determining the power curves themselves.
 Why is the y-axis given as probability instead of average run length (ARL)?
Why is the y-axis given as probability instead of average run length (ARL)?
In industry, it is common to describe the performance of QC procedures in terms of the average number of runs before a rejection signal is observed, thus the average run length is also used to describe the rejection capability of a QC procedure. In laboratories, where the objective is to detect errors in the first run in which they occur, we think it is better to describe the probability of rejecting a run. Analysts intuitively understand that a high probability is desired for error detection and a low probability for false rejection. Corresponding ARL figures can be calculated as 1/Ped and 1/Pfr, thus the desired ARL for unstable performance is 1.1 (1/0.90) and the desired ARL for stable performance is 20 to 100 (1/0.05 or 1/0.01).
 Why aren't the power curves smooth?
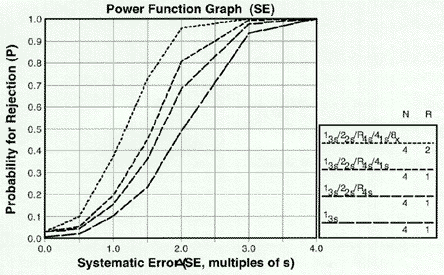
Why aren't the power curves smooth?
They should be. However, in using computer simulation, we have estimated the probabilities at distinct sizes of errors and presented point-to-point power curves for systematic errors corresponding to shifts of 0.0, 0.5, 1.0, 1.5, 2.0, 3.0, and 4.0 times the SD or CV of the method, and random errors corresponding to 1.0, 1.5, 2.0, 2.5, and 3.0 fold increases in the SD or CV of the method.[Note: later versions of the software do indeed have "smooth" curves]
How good are the probabilities estimated by computer simulations?
The probabilities estimated by computer simulation studies are subject to some experimental uncertainty and depend on the number of runs simulated for each error condition. In our work, we have generally used 1000 runs and expect the uncertainty to be about 0.01 to 0.02 for the probability of false rejection and up to 0.05 for the probability of error detection. Therefore, small differences between the estimated performance characteristics of different QC procedures should not be over-interpreted.
Why is a Ped of 0.90 considered to be ideal?
We set a general objective of achieving a Ped of 0.90 because that will generally mean that a critical error will be detected in the first run in which it occurs (actual average run length would be 1.1). Achieving higher error detection is often very costly because the power curves plateau as they approach the perfect error detection of 1.0. Going from 0.90 to 0.95 or 0.99 could require doubling the number of control measurements, thus doubling the cost of QC.
