Guest Essay
Is GUM injurious? - Or just superfluous?
- Editor's note
- Abstract
- Introduction
- What new information can we get from GUM?
- What have we lost with GUM?
- What misunderstandings and problems are introduced by GUM?
- What errors are introduced by GUM?
- Demonstration of the uncertain value of uncertainty
- Conclusion
- References
1 Department of Clinical Biochemistry, Odense University Hospital, Odense, Denmark
2 NOKLUS, Norwegian centre for external quality assurance of primary care laboratories, Division for General Practice, University of Bergen, Norway.
3 Department of Clinical Biochemistry, Vejle County Hospital, Vejle, Denmark
4 department of Clinical Biochemistry, Roskilde Hospital, Roskilde, Denmark.
Correspondence to
Per Hyltoft Petersen,
Department of Clinical Biochemistry,
Odense University Hospital,
DK-5000 Odense C.
Phone: +45 6541 2836
Fax: +45 6541 1911
Please Note: This is a translation and adaptation from a Danish paper in “Klinisk Biokemi i Norden”: “Er GUM skadelig ? - eller blot overflødig” Klinisk Biokemi i Norden 2003; 15(2): 27-31. Published here by special permission.
Editor’s Note
Here is a discussion of the concept of “uncertainty” and its implementation through the Guide to Uncertainty in Measurements (GUM).
US readers may wonder about the relevance of this topic because GUM is not widely known and applied in North America, however, clinical chemists in Europe have been concerned about its implementation for several years. As ISO standards become more widely used for accreditation of laboratories worldwide, GUM will become more widely used by both laboratories and manufacturers. ISO emphasizes the use of “trueness” and “uncertainty” to describe the quality of measurement processes, instead of our more traditional concepts of total error, accuracy, and precision.
- Trueness is used by ISO to describe the "closeness of agreement between the mean obtained from a large series of results of measurement and a true value." The emphasis on the "mean obtained from a large series of results of measurement" limits this concept to the systematic error or inaccuracy (bias) of a method.
- Uncertainty is used by ISO to describe a "parameter, associated with the result of a measurement that characterizes the dispersion of the values that could reasonably be attributed to the measurand." This term could be quantitatively described by calculating a standard deviation or some multiple (confidence interval).
In short, the new ISO terminology recommends trueness instead of accuracy, inaccuracy, or systematic error and uncertainty instead of random error, imprecision, or precision. Total error wouldn't exist! Furthermore, estimates of uncertainty would combine different sources and estimates of both random error and systematic error through propagation of errors calculations. These calculations would require a competent statistician, a clinical chemist with some mathematical or statistical aptitude, or a special computer program that could be used by laboratory analysts. Finally, as we have discussed previously on this website, there is a concern whether these new numbers have any practical usefulness (see To be Uncertain or In Error? That is the question ). That’s why we invited this commentary from a distinguished group of Scandinavian clinical chemists.
Abstract
GUM (Guide to Uncertainty in Measurements) was introduced in 1993 and is now often erquired for accreditation of laboratories in Europe. Of interest in this discussion are the following questions: - What new information can we get from GUM ?
- What have we lost with GUM ?
- What misunderstandings and problems are introduced?
- Which errors are introduced?
It is our position that the GUM definition of uncertainty, which includes the estimates of bias as well as precision, is not a useful description of the performance of a method. For example, in the case of different lots of reagents or different kits, bias is often unknown (which is different from uncertain) and the unknown bias should be estimated by use of matrix-correct controls with reference method values or patient samples measured by both reference- and field-method. These kinds of biases should not be described by a wider expanded uncertainty, but estimated and compared to analytical quality specifications for acceptable bias.
It is also demonstrated that the same value of uncertainty may cover either imprecision or unknown bias. For fasting plasma glucose, the percentage of “low risk” men over 60 years of age and BMI>27 as measured above 7.0 mmol/l is increasing from 0.8 % in the error-free situation to either 2.3 % for pure imprecision or to 10.7% or 14.3% (dependent on the calculation method) by pure bias, both described as expanded uncertainty of 10%. Thus, the same value of uncertainty may result in considerable different clinical outcomes, whether the uncertainty covers imprecision or (unknown) bias.
Our conclusions are:
- We do not have any new useful information from GUM
- We have lost an important and useful tool to distinguish between imprecision and bias.
- GUM has introduced many uncertainties in the error concept and introduced several unanswered questions.
- GUM gives erroneous information for the clinical interpretation of laboratory data.
Consequently: GUM is not only superfluous, but it is also injurious.
Introduction
GUM (Guide to Uncertainty in Measurement) [1] is a new concept, which since its introduction in 1993 has gained increasing influence in clinical biochemistry. In some countries it is recommended to express measurement uncertainty according to GUM by an established budget when dealing with accredited quantities, even though it is not directly required in the standards ISO 15189 and ISO 17025. The calculations are demanding, and even though clinical chemists such as Jesper Christensen have tried to alleviate the work [2], it is still a complex task.
The idea with GUM is to establish a common method for description of quality. The method is to convert all discrepancies to variances/ standard deviations/ coefficients of variation, which are summed up to one “universal uncertainty”. This also includes variation attributed to a corrected bias, a converted unknown bias, and all other non-quantified contributions. All these components are – together with assumed uncertainties - combined into one estimate of imprecision, which is now called uncertainty and expanded uncertainty.
What new information can we get from GUM?
The system is complicated because it is based on many theoretical contributions to the final estimate of uncertainty. In this respect GUM is static without current interest and shows, at the best, the conditions during artificial conditions at an earlier time.
GUM was introduced as a tool to investigate the weakest point in the uncertainty chain by investigation of variances, but it is not necessary for that application since we have performed analyses of variance for the same purpose for thirty ears. Further, the application of the “cause-and-effect diagram” also called ‘fish-bone diagram’ is claimed to be new, but it has been used in clinical chemistry since 1990.
GUM may be superior for describing the uncertainty of reference methods, but this has little impact in the routine clinical biochemistry laboratory.
What have we lost with GUM?
With introduction of GUM, we have lost the ability to differentiate between different types of analytical errors that have different effects on the actual quality of analyses. We have lost the information about the individual components of bias, imprecision, interference, specificity etc. GUM requires that all these errors be collected into one unspecified variable, the uncertainty according to GUM. Thus, GUM hides the information about individual components of error.
We are certainly interested in avoiding analytical bias of a certain size, rather than including it in an estimate of uncertainty. We know our analytical methods are subject to systematic changes and that we can monitor those changes via internal quality control, IQC, in order to detect systematic errors and eliminate them through corrective action.
If we follow GUM and just describe these conditions and thus accept that uncertainty grows, then the outcome is unpredictable and the resulting quality unsatisfactory.
What misunderstandings and problems are introduced by GUM?
According to GUM, all errors are part of uncertainty, although this is not a correct term. An example: if you place a die inside a box and shake it, there are six possible outcomes. When the die is thrown, but the result is kept hidden by the box, the outcome is not uncertain, but unknown. The unknown result can be disclosed by removing the box. This is different from uncertainty. The steps are then, uncertain, unknown, known.
The traceability chain from reference method to analyses in the laboratory can be regarded a similar process. For every step, after the reference method, bias may be estimated. It is unknown, but can be measured by investment of time and money. The more replicates, the narrower the confidence interval and the more expensive.
Thienpont et al. [3] have investigated what quantities can theoretically be described by GUM. This was done by distinguishing between so called SI analytes, which theoretically are traceable to a well defined component and a reference method, and all the other components, which are not well defined or decided by a reference method. SI analytes, may in principle, be described by GUM. There are 30 to 40 quantities such as electrolytes and simple metabolites. The rest are free analytes, as for instance, ionised calcium, “families” of molecules with minor or larger deviations, e.g., proteins (IgG consists of more than 10x106 different molecular forms) and hormones (often components with quantification based on reference preparations given in International units, IU such as hCG). Thus, GUM may be useful only for a minority of quantities.
Even for SI analytes, the traceability chain usually involves materials whose matrix is manipulated in different ways, as well as analytical methods that are matrix dependent, thus introducing biases into the traceability chains. To correct for this, split sample measurements in large numbers of patient samples should be used, which will however, violate the idea of the traceability chain.
Further difficulties are found in external quality control or peer assessment (even for the SI analytes), where matrix correct materials and reference method values are used. This introduces a discrepancy between the interpretation of control material results from matrix correct materials with reference method concentrations and our kit with unknown bias from the rather long traceability chain with manipulated and non-commutable matrixes. The bias will not be discovered until the external control shows it.
What should be done, when a bias is disclosed by the high quality external control?
- Make a new calibration with the calibrators? This will however, not help, if the problem is manipulated materials for calibration.
- Recalibrate, guided by the results of the control investigation? This could be attempted but is not allowed, although the control is located hierarchically higher.
- Calibrate by use of national or regional reference preparations of same high quality as the control? Actually, this is done in the Nordic Reference interval-project [4].
- Extend the confidence interval? This would be legal according to GUM, although there is a issue of whether that provides any practical value.
What errors are introduced by GUM?
GUM has been declared the only model for combining bias and imprecision, although several methods are well known. All of them including GUM have disadvantages and advantages, which are not solved by GUM [5]. The safests way to describe quality is to identify bias and imprecision separately both conceptually and also experimentally. This correlates with their individual influence on the clinical outcome of results. It is still true, as Box and Luceño [6] said ‘that all models are wrong, but some models are useful’. In that regard, GUM is less useful than our traditional models.
Here are some examples from clinical biochemistry that illustrate how GUM will introduce wrong estimates by interpreting bias into uncertainty.
I. In Denmark it is allowed for general practitioners to measure INR in their practice. If each general practitioner should have effective control service, this would be an economic catastrophe and an enormous workload. Consequently, each new batch-number of INR-kits is tested for bias and imprecision in accordance with analytical quality specifications. This is done by analysing 40 patient samples as split samples in accordance with a defined Danish reference method. In agreement with the kit distributors, only kits fulfilling the goals for bias and imprecision can be sold. Each batch number has a well-defined bias, which can be taken notice of, but only if it is known. Because of the large number of samples the confidence interval will be small so the lot can be validated, while the bias according to GUM can be hidden by creation of a larger uncertainty.
II. Thienpont et al. have oberved a mean bias of + 5.1% for cholesterol in serum in the Czech Republic [7]. With this bias of this magnitude, about 10 % more cases of hypercholesterolaemia will be identified than if no bias were present. Lumping the bias into the estimate of uncertainty won’t improve clinical practice, but eliminating that bias will. That’s why it is important to maintain out traditional models and tools that are useful for improving quality.
III. Kallner has calculated the uncertainty in measurements of blood glucose [8] and identified a combined relative uncertainty of 14%. With a multiplying factor of 2 to describe 95% uncertainty, i.e., an uncertainty of 28 % in the result, a true value of 5.5 mmol/l refers to a true value between 4.0 and 7.0. Quite interesting, but not useful clinically!
IV. Linko et al. (9) have demonstrated that for glucose, the inclusion of the biological within-subject variation will give an expanded uncertainty of 14 %. This is half of the Kallner-value. More interesting is the estimate for two other glucose estimates (without including biologic variation) with results for expanded uncertainty of 2.4% vs.2.6%. Also this is interesting, although unrealistic. It is thus possible to obtain both too large and too small uncertainties, even though these estimates are made by the proper methodology and with best intentions.
Demonstration of the uncertain value of uncertainty
Let us consider the usefulness of these estimates of uncertainty in cases where laboratory tests are used for monitoring and diagnosis.
In monitoring, the difference between two consecutive measurements is often very valuable. The measured difference is usually compared to a Reference Change Value (RCV), which can be calculated from 1.96*2½*CV, where 1.96*CV matches the expanded uncertainty, CV is the biological within-subject variation (here approximately 5 % for glucose) and 2½ accounts for the two measurements. RCV is thus 14 %, but according to Kallner and Linko it will amount 2½*40% and 2½*20%, respectively. In addition, a method bias will influence equally on both results if analysed on the same instrument. As a consequence, RCV becomes an unrealistic large value and is not at all useful in understanding when a change in patient test values is clinically important.
In diagnosis, Jørgensen et al. have found that concentrations of plasma glucose in healthy women are lower than for healthy men and that the concentrations increase with age and BMI (10). If a low risk group of males aged above 60 years and with a BMI above 27 kg/m2 is considered, then the risk of having measured a plasma glucose above 7.0 mmol/L is 0.8% in the error free situation.
Let us consider the effects of expanded uncertainties of 5% or 10% according to GUM for two different sources of uncertainty:
- That the uncertainty is due to random errors – imprecision – exclusively;
- That the uncertainty is due to positive bias exclusively – calculated according to GUM and as total.
The effect on the proportion of patients having glucose values above 7.0 mmol/L is shown in Table 1 and Figure 1 below:
Table 1
Percentage plasma glucose measured above 7.0 mmol/l of males belonging to a ‘low risk’ population aged above 60 years with a BMI above 27 kg/m2. The percentage of uncertainty is given as expanded uncertainty of 5% and 10%, calculated as imprecision and bias exclusively. For imprecision is calculated E = 2*CV (corresponding to CV = 2.5 % and 5 %, respectively) and for unknown bias according to GUM: E = 2* (a/3½). The result is a = E*3½/2, i.e. 4.3 % and 8.7 %, while “known“ bias is 5 or 10%
| Uncertainty Expanded | Imprecision Exclusively | Bias GUM | Bias exclusively |
| No error | 0.8% | 0.8% | 0.8% |
| 5% | 1.2% | 3.5% | 4.2% |
| 10% | 2.3% | 10.7% | 14.3% |
Results for expanded uncertainty of 5 % are illustrated in Figure 1
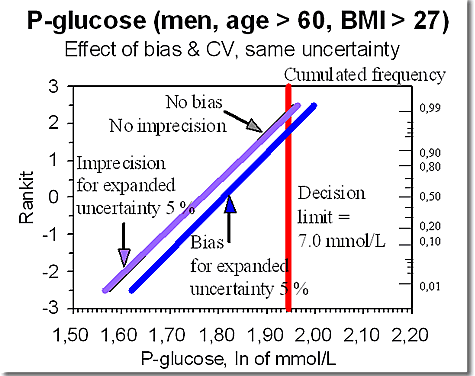
The distribution of plasma glucose for males aged above 60 years and with BMI above 27 kg/m2 given as a line in Rankit plot. The abscissa is in mmol/L, and the vertical line indicates plasma glucose of 7.0 mmol/L.The distribution is shown for the situation without errors (black line, no bias, no imprecision) together with two situations both with expanded uncertainty = 5%: Expanded uncertainty is here exclusively referable to random errors (purple line), nearly indistinguishable from the error-free situation, and also for the situation where expanded uncertainty can be exclusively referred to systematic errors (the blue line at the right) = the line with a larger number of healthy low risk cases and plasma glucose > 7.0 mmol/l.
This example demonstrates that clinical outcomes may be very different with the same expanded uncertainty, if the result is based on exclusively random vs. systematic errors. That is in case of unknown errors. When buying a kit or a calibrator, the uncertainty should be included in the information. For the user however, this is a bias that can become known by the split-sample-principle or matrix correct control materials – but it is unknown until that is investigated.
The uncertainty measure is not informative, because also a bias is given as an uncertainty, and the clinical outcome based on a bias (not estimated) will become different from the outcome based on random variation with the same uncertainty value.
Thienpont et al. found a mean bias of +3.7% for plasma glucose in the Czech Republic [7]. This corresponds to 3% more low-risk males above 60 years and with BMI above 27 kg/m2. It sounds small, although it will become quite a great number of cases in the whole country or in the European Union.
The huge difference between the effect of bias and imprecision on biological and clinical situations is described in a large number of articles that have apparently have gone unnoticed. For example, here are two recent publications in Scand J Clin Lab Invest [11, 12].
Conclusion
- GUM does not provide a new useful tool for characterizing and understanding the performance of analytical methods in clinical biochemistry. On the contrary, GUM considers different types of errors (precision and accuracy) as if they were the same.
- With the use of GUM, we lose a differentiated and operational tool that made bias and imprecision distinguishable, so that error detection was easy and the influence of the two types of error was clear.
- GUM has introduced a series of unanswered questions, mainly by describing an unknown (not measured) bias as uncertainty.
- GUM causes errors in the clinical use and interpretation of laboratory tests. The unknown bias, which is introduced with each batch of a kit, is by GUM interpreted as a standard deviation or a coefficient of variation. The effect of the error on clinical outcome is thus underestimated, which may be dangerous for the clinical interpretation of laboratory data.
In summary, GUM is not just superfluous, GUM is dangerous because the interpretation of data according to GUM may distort the biochemical result and thus the clinical outcome.
References
- Guide to expression of uncertainty in measurement. ISO: Geneva 1995.
- Kristiansen J. Description of a generally applicable model for the evaluation of uncertainty of measurement in clinical chemistry. Clin Chem Med Lab 2001; 39:920-31.
- Thienpont LM, van Uytfanghe K, de Leenheer AP. Reference measurement systems in clinical chemistry. Clin Chem Acta 2002; 323:73-87.
- http://www.furst.no/norip/
- Hyltoft Petersen P, Stöckl D, Westgard JO, Sandberg S, Linnet K, Thienpont L. Models for combining random and systematic errors. Assumptions and consequences for different models. Clin Chem Lab Med 2001; 39:589-95.
- Box G, Luceño A. Statistical Control by monitoring and feedback adjustment. John Wiley & sons, INC, New York – Chichester – Weinheim – Brisbane – Singapore – Toronto 1997
- Thienpont LM, Stöckl D,Kratochvila J, Friedecký, Budina M. Pilot external quality assessment survey for post-market vigilance of in-vitro diagnostic medical devices and investigation of trueness of participants’ results. Clin Chem Lab Med 2003; 41:183-6.
- Kallner A. Quality specifications based on the uncertainty of measurements. Scand J Clin Lab Invest 1999; 59:513-6.
- Linko S, Örnemark U, Kessel R, Taylor PDP. Evaluation of uncertainty of measurement in routine clinical chemistry – Applications to determination of the substance concentration of calcium and glucose in serum. Clin Chem Lab Med 2002; 40:391-8.
- Jørgensen LGM, Stahl M, Brandslund I, Hyltoft Petersen P, Borch-Johnsen K, de Fine Olivarius N. Plasma glucose reference interval in a low-risk population 2. Impact of the new WHO and ADA recommendations on diagnosis of diabetes mellitus. Scand J Clin Lab Invest 2001; 61:181-190.
- Hyltoft Petersen P, Fraser CG, Kallner A, Kenny D (eds). Strategies to Set Global Analytical Quality Specifications in Laboratory Medicine. Scan J Clin Lab Invest 1999; 59:475-585.
- Hyltoft Petersen P, Brandslund I, Jørgensen LGM, Stahl M, de Fine Olivarius N, Borch-Johnsen K. Evaluation of systematic and random factors in measurements of fasting plasma glucose as the basis for analytical quality specifications in the diagnosis of diabetes. 3. Impact of the new WHO and ADA recommendations on diagnosis of diabetes mellitus. Scand J Clin Lab Invest 2001; 61:191-204.
