Six Sigma
Standardizing the Sigma-metric
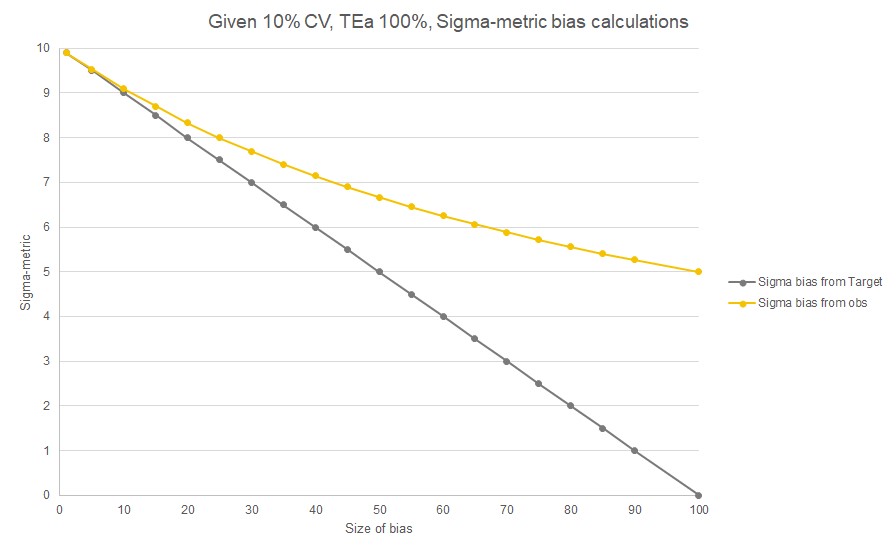
As the Sigma-metric grows in popularity and usefulness, scrutiny on the calculation has grown. The time for standardizing the Sigma-metric, as much as can be done, is upon us.

As the Sigma-metric grows in popularity and usefulness, scrutiny on the calculation has grown. The time for standardizing the Sigma-metric, as much as can be done, is upon us.