Basic QC Practices

This lesson discusses the math involved with QC practice. Despite the age of computers, we still have to crunch the numbers ourselves sometimes. Dr. Westgard discusses the terms Mean, SD, CV, Control Limits, z-scores and SDI's, explaining what they are, giving the equations, and demonstrating how to calculate them.

• What calculations?!
• Mean, SD, CV
• Control Limits
• Cumulative or lot-to-date calculations
• Z-scores, SDI's

PLEASE NOTE: an updated version of this lesson is available in Basic QC Practices, 3rd Edition

What Calculations?

Are any calculations necessary if the control material has an assay sheet that lists the range of acceptable values for my method?

Yes, you still need to collect your own control measurements and calculate the control limits that apply in your own laboratory. Values and limits found on assay sheets often describe the performance observed by a specific method in several different laboratories, which means that the figures are likely to include variations that occur between laboratories. Therefore, those limits are likely to be too wide for an individual method in your laboratory. If the control limits are too wide, you won't be able to detect problems in your own laboratory.

Note that US CLIA regulations require that the laboratory determine it's own mean and standard deviation. [493.1218(5d) "When calibration or control materials are used, statistical parameters (e.g., mean and standard deviation) for each lot number of calibration material and each lot of control material must be determined through repetitive testing."]

What statistics need to be calculated to establish my own control limits? You need to calculate the mean and standard deviation from the control results that have been collected for each control material. It's also common to express the standard deviation in percent by calculating a coefficent of variation, or CV.

Mean, SD, CV

How many control measurements should be collected before making these calculations?

The rule of thumb is to collect at least 20 measurements over at least 2 weeks or 10 working days, and preferably over at least 4 weeks or 20 working days. You do this by including control materials as part of your daily work for a long enough period to observe the variation expected in your laboratory. Too short a period leads to too small an estimate of the standard deviation. Longer is usually better because the estimates will include more operators and more method changes, such as pre and post maintenance performance, changes in reagent lot numbers, sample probes or pipettes, etc., thus even one month might be too short a period. In practice, calculations of the mean and standard deviation are often made monthly and then the monthly data are added to data from previous months to calculate the cumulative or lot-to-date mean and standard deviation that are then used for setting control limits. These cumulative or lot-to-date control limits are a better representation of long term test performance.

How many significant figures are needed in the control results that are used to estimate the mean and standard deviation?

Control results should have at least one more significant figure than the values reported for patient test results in order to get good estimates of the mean and standard deviation and to be able to set appropriate control limits. With some instrument systems where test results are rounded for clinical significance, only whole numbers end up being reported for control results, thereby giving a discrete distribution of control values with only a few possible results, rather than the continuous gaussian distribution that is expected. This may lead to some practical problems in setting control limits because the calculated control limits may not correspond to the discrete integer values being reported.

What is the equation for the mean?

The mean is determined by adding a group of measured values, then dividing the total by the number of measurements in the group. This is often written as:

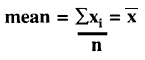
where the mean may be symbolized by, 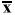an x with a bar over it (hence the term x-bar), x_i represents an individual measurement, 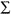represents the operation of summation or addition of all these x_i values, and n is the number of x_i values in the group. Using just 3 numbers for an example (which is not sufficent data according to the current laboratory practice of obtaining a minimum of 20 results), for the values of 100, 105, and 98, 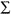x_i is the total of these three or 303, and the mean or average is 303/3 or 101.

What's a practical way to calculate the mean?

Hand held calculators can be used to easily calculate the total of a group of measurements, then divide that total by the number of measurements included. Scientific calculators usually have a built-in program for both the mean and standard deviation. Electronic spreadsheets, such as Lotus 1-2-3 and Excel, usually have built-in functions for calculating the mean and standard deviation from a column of data. Statistical programs, such as Minitab, SPSS, SAS, and Systat have functions for calculating the mean and standard deviation, as well as describing the population in terms of the observed median, mode, range, lowest value, highest value, etc.

In most laboratories, the QC program in the laboratory computer system will calculate the control data captured on-line or through manual entry. The QC programs incorporated in instrument systems and some Point-of-Care devices have similar capabilities. Stand alone QC programs on personal computers are also available and offer complete support for calculations, graphic displays of control charts, and storage of results. Participants in external survey programs offered by instrument or control manufacturers can also submit their control data for analysis by the vendors, though the data analysis may require up to a month for return of the results.

What does the mean tell me about method performance?

The mean value for a control material provides an estimate of the central tendency of the distribution that is expected if method performance remains stable. Any change in accuracy, such as a systematic shift or drift, would be reflected in a change in the mean value of the control, which would be shown by a shift or drift of the distribution of control results. Always keep in mind that the mean is related to accuracy or systematic error and the standard deviation is related to precision or random error. See QC - The Idea for a review of how the mean of the distribution of control results is related to the mean and control limits on a control chart.

What is the equation for the standard deviation?

The standard deviation is determined by first calculating the mean, then taking the difference of each control result from the mean, squaring that difference, dividing by n-1, then taking the square root. All these operations are implied in the following equation:

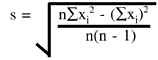
where s represents the standard deviation, 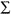means summation of all the (x_i -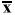)² values, x_i is an individual control result,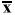is the mean of the control results, and n is the total number of control results included in the group.

For computerized calculations and for estimating the cumulative standard deviation, the form of the equation that is commonly used is:

where 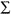x_i² is the summation of all the squared individual values, and (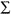x_i)² is the square of the sum of all the individual values.

What's a practical way to calculate the standard deviation?

It is easy to use a scientific calculator, an electronic spreadsheet, or a statistics program, all of which have built-in functions for calculating the standard deviation of a group of measurements. This function for calculating the standard deviation is often labeled "SD". Specialized QC software in laboratory information systems, instruments, and personal computer workstations will automatically calculate the standard deviation for the data being accumulated. External quality assessment programs offered by manufacturers of instruments and control materials will also process the data of participants and provide reports that include the calculated results.

What does the standard deviation tell about method performance?

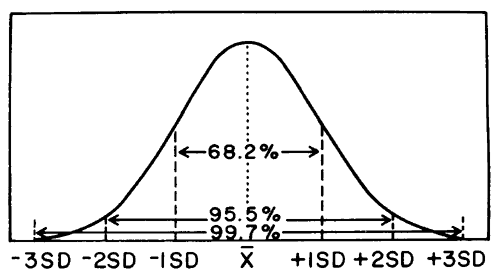
The standard deviation is related to the spread or distribution of control results about the expected mean. Whereas the mean is an indicator of central tendency and therefore related to accuracy or systematic error, the standard deviation is a measure of the width of the distribution and is related to imprecision or random error. The bigger the standard deviation, the wider the distribution, the greater the random error, and the poorer the precision of the method; the smaller the standard deviation, the narrower and sharper the distribution, the smaller the random error, and the better the precision of the method.

For a measurement procedure, it is generally expected that the distribution of control results will be normal or gaussian, as shown above. For a gaussian distribution, the percentage of results that are expected with certain limits can be predicted. For example, for control results that fit a gaussian distribution, it would be expected that 68.2% of the observed results will be within plus/minus 1s of the mean; 95.5% within plus/minus 2s of the mean, and 99.7% within plus/minus 3s of the mean.

What's a CV?

CV refers to the "coefficient of variation," which describes the standard deviation as a percentage of the mean, as shown in the following equation:

CV = (s/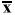)100

where s is the standard deviation, 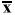is the mean, and the multiplier of 100 is used to convert the s/ 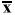ratio to a percentage.

Why is a CV useful?

The standard deviation of a method often changes with concentration, i.e., the larger the concentration, the larger the standard deviation, therefore it is usually necessary to estimate the standard deviation at the concentration level of interest. Because the CV reflects a ratio of the standard deviation to the concentration, it is often provides a better estimate of method performance over a range of concentrations.

For example, you may be interested in planning a QC procedure on the basis of the performance needed at a critical decision concentration of 200 mg/dL, but the nearest control available has a mean of 190 mg/dL. Therefore, it is best to calculate the CV from the observed results at 190 mg/dL, then apply that CV to the 200 mg/dL decision level. This is the reason that QC planning applications with the QC Validator program use a percentage figure for the imprecision of the method.

Control limits

How do you calculate control limits?

Given the mean and standard deviation for a control material, control limits are calculated as the mean plus and minus a certain multiple of the standard deviation, such as 2s or 3s. For cholesterol where a control material has a mean of 200 mg/dL and a standard deviation of 4 mg/dL, the 2s control limits would be 192 and 208 mg/dL, and the 3s control limits would be 188 and 212 mg/dL.

See a web-based Control Limit calculator in the lesson, QC - The Levey-Jennings Chart

How many significant figures should be used in control limit calculations?

As a rule of thumb, the control results and the calculated standard deviation should have at least one more significant figure than needed for clinical significance of the patient test result; the mean of a control material should include at least two more significant figures than needed for clinical signficance of the patient test result. When in doubt, carry more significant figures than necessary and round at the end when the control limits have been calculated. Most calculators and computers carry plenty of extra figures so you can round at the end.

Cumulative or lot-to-date calculations

What's a cumulative or lot-to-date control limit?

Typically, control results are summarized by calculating the mean, standard deviation, CV, and N on a monthly basis. In order to establish longer term estimates of the mean and standard deviation, the control data or calculated results need to be accumulated to describe performance observed over a longer periods of time. Longer term limits are often described as "cumulative limits," which indicates they have been calculated from cumulative means and standard deviations. These may also be referred to as "lot to date" limits when these calculated values are provided by a manufacturer or supplier who processes the control data for a group of laboratories in order to provide information about the comparative performance between laboratories and between methods.

What's a cumulative standard or lot-to-date deviation?

This is a long term estimate of a method's precision performance based on a large number of control measurements collected over a long period of time. A long period here is at least two months and could be several months, even a year.

How is a cumulative or lot-to-date standard deviation calculated?

These calculations are often automatically performed by the QC programs in laboratory computer systems, personal computer work stations, and in many automated instruments and even some point-of-care devices.

If you need to perform these calculations yourself, one practical approach is to calculate monthly statistics, then tabulate the month n's, x_i and x_i², which can then be totaled and used in the equation below to provide the cumulative estimate:

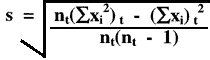
where n_t(x_i)t² is the total of the sums of all the squared individual values, and (x_i)t² is the square of the total of the sums of all the individual values, and n_t is the total number of measurements in the time period of interest.

What's a cumulative or lot-to-date mean?

This is a long term estimate of the central tendency observed for a control material based on a large a number of control measurements collected over a long period of time. A long period here is at least two months and could be several months, even a year. Changes in the accuracy of a method could lead to shifts or drifts in the mean observed for a control material.

How is a cumulative or lot-to-date mean calculated?

From the monthly statistics that are calculated, tabulate the monthly n's and x_i's, which can then be totaled for the period of interest (two months, several months), and used in the equation below to provide the cumulative mean:

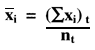
Where (x_i)_t is the total of the monthly sums of individual values and nt is the total of the monthly ns for the period of interest.

How are cumulative or lot-to-date control limits calculated?

The estimates for the cumulative or lot-to-date mean and standard deviation, as calculated above, are used to calculate cumulative or lot-to-date control limits. Here's a table that illustrates the whole procedure.
(Cumulative results are show in parentheses.)

Month	Monthly total (cumulative total)			Calculated statistics		Control Limits
	n	x	x2	Mean	s	Mean +/- 3s
1	20	3983	793465	199.15	3.63	188.3 - 210.0
2	20	3993	797537	199.65	4.20	187.1 - 212.2
	(40)	(7976)	(1591002)	(199.40)	(3.86)	(187.8 - 211.0)
3	20	4002	801138	200.10	4.22	187.5 - 212.7
	(60)	(11978)	(2392140)	(199.63)	(3.97)	(187.7 - 211.6)
4	20	4020	808182	201.00	2.92	192.2 - 209.8
	(80)	(15998)	(3200322)	(199.96)	(3.77)	(188.7 - 211.3)
5	20	3995	798259	199.75	3.68	188.7 - 210.8
	(100)	(19993)	(3998581)	(199.93)	(3.73)	(188.7 - 211.1)

See a web-based QC calculator that performs these calculations.

Z-scores and SDI's

What's a z-score?

A z-score is a calculated value that tells how many standard deviations a control result is from the mean value expected for that material. It is calculated by taking the difference between the control result and the expected mean, then dividing by the standard deviation observed for that control material. For example, if a control result of 112 is observed on a control material having a mean of 100 and a standard deviation of 5, the z-score is 2.4 [(112- 100)/5]. A z-score of 2.4 means that the observed control value is 2.4 standard deviations from its expected mean, therefore this result exceeds a 2s control limit but not a 3s control limit.

Why is a z-score useful?

It is very helpful to have z-scores when you are looking at control results from two or more control materials at the same time, or when looking at control results on different tests and different materials on a multitest analyzer. You can quickly see if any result exceeds a single control limit, for example, a z-score of 3.2 indicates that a 3s control limit has been exceeded. You can also look for systematic changes or trends occurring across different control materials, for example, consecutive z-scores of 2 or greater on two different control materials.

What's an SDI?

If you participate in an external quality assessment program or a proficiency testing program, you are asked to analyze a series of unknown specimens and submit your test results for comparison with those obtained by other laboratories. The data from all the laboratories are usually analyzed to determine an overall average and standard deviation for the group. The program will generally report your performance relative to the group. The difference between your test results and the overall average is often expressed by a standard deviation index, or SDI, which expresses the difference in terms of the number of standard deviations from the overall mean. For example, an SDI of 1.0 would indicate your result fell one standard deviation from the mean. On a series of specimens, if you observe SDIs such as +1.5, +0.8, +2.0, +1.4, and +1.0 (all positive), this suggests that your method is generally running on the high side and is biased, on average, by +1.3 SDI. To figure the size of this average bias in concentration units, you need to multiply by the actual value of the group SD.

Note the similarity between the calculation of the SDI and the z-score. They're basically the same thing, but the z-score tends to be used in internal QC programs to compare an individual QC result with the expected values for that material, whereas the SDI tends to be used in external QC programs to compare the performance of the lab with the overall mean for a defined comparative group or with an established target value.

Why's an SDI useful?

One advantage is that it allows you to inspect results from many different tests at the same time, without having to think about different units and the actual magnitude of the change in the units of the test. In general, any SDI of 2.0 or greater deserves some special concern, regardless what the test is. Any test whose average SDI is 1.0 or greater deserves some special attention because your method shows a systematic difference from the group. In the future, this bias might lead to unacceptable results.